Hi,mathematics lovers,edisi terbaru kali ini adalah kisi-kisi soal uts matematika
untuk siswa kelas VII semester genap.
Kisi-kisi berikut hanyalah bayangan soal yang akan kalian hadapi sebagai
sumber belajar matematika.Setidaknya kalian sudah memiliki metode belajar
matematika mulai dari latihan soal hingga mengumpulkan informasi melaui internet.
Tanpa panjang lebar, kita lihat sama sama yuk soal-soalnya.
Ini dia...
1.Diantara kumpulan-kumpulan berikut, yang merupakan himpunan adalah . . .
A. Kumpulan hewan berkaki empat
B. Kumpulan wanita cantik di Indonesia
C. Kumpulan lautan yang luas
D. Kumpulan binatang yang sangat kecil
2.A adalah himpunan bilangan prima kurang dari 15.
Bila A dinyatakan dengan mendaftar anggotanya maka berikut ini yang benar adalah . . .
A. A = {2,3,5,7,9,11,13}
B. A = {2,3,5,7,11,13}
C. A = {3,5,7,11,13,15}
D. A = {3,5,7,9,11,13,15}
3. Diketahui:
A= {u, n, t, a}
B= {1,2,4}
C = {1,4,9,16,25}
Manakah pernyataan berikut yang BENAR?
A. 2 ∈ A
B. u ∉ B
C. 25 ∈ B
D. 9 ∉ C
4. K adalah himpunan bilangan genap kurang dari 12 maka n (K) = . . .
A. 5
B. 6
C. 7
D. 8
5. Berikut ini yang termasuk himpunan kosong adalah . . .
A. M ={0}
B. N = Himpunan bilangan ganjil yang kurang dari1.
C. P = Himpunan nama bulan yang berjumlah 28 hari.
D. Q = Himpunan bilangan prima yang genap.
6. Semesta pembicaraan dari B = { 2,3,5,7,11} adalah . . .
A. Bilangan prima kurang dari 11.
B. Bilangan prima kurang dari 13.
C. Bilangan ganjil yang kurang dari 13.
D. Bilangan asli kurang dari 11.
7. Diketahui:
K = {1,3,5}
Semua himpunan bagian dari K adalah . . .
A. { },{1},{3},{5}
B. { },{1},{3},{5},{1,3},{1,5}
C. { }, {1},{3},{5},{1,3},{1,5},{3,5}
D. { },{1},{3},{5},{1,3},{1,5},{3,5},{1,3,5}
8. Berapa banyakkah semua himpunan bagian dari:
Q = {bilangan genap kurang dari 10}
A. 5
B. 8
C. 16
D. 32
9. Diketahui:
A = {bilangan prima kurang dari 15}
B = {bilangan ganjil kurang dari 14}
Dengan mendaftar anggota-anggotanya maka anggota dari A ∩B = . . .
A. {2,3,5,7,9,11,13}
B. {3,5,7,9,11,13}
C. {3,5,7,11,13}
D. {3,5,7,11,13,15}
10.Diketahui:
P = { x | 2 ≤ x ≤ 8 x ∈ bilangan asli}
Q = { x | 2 ≤ x ≤ 7, x ∈ bilangan prima }
Dengan mendaftar masing-masing anggotanya, maka n (P ∪ Q) = . . .
A. 4
B. 5
C. 6
D. 7
11.Jika K = {faktor dari 30} dan;
M = { x | x ≤ 11, x ∈ bilangan prima},
Dengan mendaftar masing-masing anggotanya maka anggota M – K adalah…
A. {7,11}
B. {1,2,7,11}
C. {5,6,7,11}
D. {1,6,10,15,30}
12. Jika S = { 0, 1, 2, 3, 4, . . . , 10};
R = { lima bilangan asli yang pertama};
T = { x | 2 ≤ x ≤ 10, x ∈ bilangan genap}.
Dengan mendaftar masing-masing anggotanya maka anggota dari 〖 R〗^C∩ T^Cadalah…
A. { 7, 9}
B. {0,7,9}
C. {1,3,5,7}
D. {0,1,3,5,7,9,10}
13. 8° = 〖⋯ 〗^'
A. 400 C.560
B. 480 D.640
14. 〖(( 2)/5 )〗^' = 〖⋯ 〗^''
A. 20 C. 28
B. 24 D. 30
15. 12°〖35〗^' 〖28〗^''+ 33°〖18〗^' 〖15〗^''= ⋯
A. 45°〖53〗^' 〖43〗^''
B. 45°〖35〗^' 〖43〗^''
C. 54°〖35〗^' 〖43〗^''
D. 54°〖53〗^' 〖43〗^''
16. 25°〖34〗^' 〖22〗^''- 13°〖28〗^' 〖55〗^''= ⋯
A. 12°5^(' ) 〖27〗^''
B. 12°6^(' ) 〖33〗^''
C. 12°〖27〗^(' ) 5^''
D. 12°〖33〗^(' ) 〖27〗^''
17. Sudut terkecil yang terbentuk pada jarum jam pukul 11.00 adalah . . .
A. Sudut Lancip
B. Sudut Tumpul
C. Sudut Lurus
D. Sudut Refleks
18. Sudut terkecil yang terbentuk pada jarum jam pukul 15.00 adalah . . .
A. Sudut Lancip
B. Sudut Tumpul
C. Sudut Lurus
D. Sudut Siku-siku
19. Jenis sudut apakah yang terbentuk jika sudut itu 4/5 dari sudut putaran penuh?
A.Sudut Lancip
B. Sudut Tumpul
C. Sudut Lurus
D. Sudut Refleks
ESSAY:
1. Diketahui P adalah himpunan bilangan prima kurang dari 20.
Nyatakan himpunan P di atas dengan cara:
A. Notasi pembentuk himpunan;
B. Mendaftar anggotanya.
2. Diketahui
K = { Bilangan prima kurang dari 17}
L = { x | x < 16, x ∈ bilangan ganjil}
Dengan mendaftar anggotanya, tentukan:
A. K ∩ L =
B. n (K ∩ L)
3. Dari 40 siswa dalam kelas, terdapat 22 siswa yang sudah divaksin cacar dan 15 siswa yang sudah divaksin hepatitis. Jika 10 siswa belum mendapat kedua vaksin tersebut maka banyaknya siswa yang telah mendapat kedua vaksin tersebut adalah …
Ok mathematics lover,tak ada gading yang tak retak.
Mungkin hanya sedikit soal yang penulis share,tetapi setidaknya bisa
membantu kalian dalam belajar.Akhir kata...
SELAMAT BELAJAR SEMOGA SUKSES!!!
Halaman
▼
Senin, 26 Maret 2012
Senin, 12 Maret 2012
Khusus edisi terbaru kali ini,
mathematics is easy akan mengajak pembaca
sekalian untuk menguji kemampuan kita
berimajinasi. Ini biasa di kenal dengan
salah satu bagian dari tes IQ.
Siap-siap untuk menggunakan daya imajinasimu...
Ok,kita mulai dari gambar berikut.
OK mathematics lover,apa yang kalian lihat dari gambar di atas?
Nah dengan berimajinasi, kalian akan melihat gambar nenek tua.
hehe nenek siap tuh?
Bagi kalian yang bosan lihat nenek2 nya coba berimajinasi
melihat gadis cantik dari gambar tersebut.
Hmm, so beautiful right?
Next,kita berimajinasi menemukan 11 wajah dari gambar naturalisme berikut.
Wah wah ternyata alam menyediakan pemandangan yang extraordinary.
Dari gerombolan dedaunan kita bisa melihat aneka wajah,
Dari tumpukan-tumpukan bebatuan juga bisa membentuk wajah manusia,
Nah, coba kalian cari 11 wajah dari lukisan tersebut.
Kalau udah ketemu 11 wajah berarti mathematics lover HEBAT DAH!
Dua Jempol buat you!
Ok, kita beranjak ke lukisan berikut.
Nah, di gambar ini kalian harus menemukan 9 orang.
Tentunya harus menggunakan daya imajinasimu,
atau hanya orang yang beriman yang bisa lihat,hehehehe
Udah ketemu belon mathematics lover?
Hey mathematics lover, kalian pasti tau kan hipnotis?
Nah,gambar kali ini menguji kalian menggunakan imajinasmu
untuk melihat sesuatu yang aneh,
seperti apakah?
Ini dia...Coba kalian perhatikan titik yang ada di tengah dengan seksama.
Sudah itu, kalian gerakkan kepala kalian maju mundur.
Apa yang mathematics lover lihat?
Rantainya bergerak kan?
Nah,seperti hipnotis kan?
Buktinya mathematics lover nurut nurut aja tu disuruh
gerak-gerakkan kepala,iya kan?
Ayo ngaku!!!
Lanjut,sekarang lihat gambar ini.
Nah,ini khusus bagi mathematics lovers yang tajam penglihatannya.
Kalau mathematics lover perhatikan sesaat hanya terlihat gambar vas
bunga,iya toh?
Jika kita lihat dengan teliti dari sisi gelapnya,kita akan
melihat dua sisi wajah bule alias orang asing,
Bisa lihat nggak mathematics lovers?
Ok,mathematics lover ada yang suka kelinci nggak?
Atau ada yang suka bebek nggak?
Nah ternyata kelinci ama bebek nggak jau2 beda lo...
Percaya nggak???
Ya nggak lah,masak percaya?kalau percaya berarti menduakan tuhan...
hehehe...
Nah ini dia gambarnya...
Ok Mathematics lover sampai disini dulu kita berimajinasi,
Bagi mathematics lover yang punya komentar bisa post comment di blog ini.
See you again!!!
mathematics is easy akan mengajak pembaca
sekalian untuk menguji kemampuan kita
berimajinasi. Ini biasa di kenal dengan
salah satu bagian dari tes IQ.
Siap-siap untuk menggunakan daya imajinasimu...
Ok,kita mulai dari gambar berikut.
OK mathematics lover,apa yang kalian lihat dari gambar di atas?
Nah dengan berimajinasi, kalian akan melihat gambar nenek tua.
hehe nenek siap tuh?
Bagi kalian yang bosan lihat nenek2 nya coba berimajinasi
melihat gadis cantik dari gambar tersebut.
Hmm, so beautiful right?
Next,kita berimajinasi menemukan 11 wajah dari gambar naturalisme berikut.
Wah wah ternyata alam menyediakan pemandangan yang extraordinary.
Dari gerombolan dedaunan kita bisa melihat aneka wajah,
Dari tumpukan-tumpukan bebatuan juga bisa membentuk wajah manusia,
Nah, coba kalian cari 11 wajah dari lukisan tersebut.
Kalau udah ketemu 11 wajah berarti mathematics lover HEBAT DAH!
Dua Jempol buat you!
Ok, kita beranjak ke lukisan berikut.
Nah, di gambar ini kalian harus menemukan 9 orang.
Tentunya harus menggunakan daya imajinasimu,
atau hanya orang yang beriman yang bisa lihat,hehehehe
Udah ketemu belon mathematics lover?
Hey mathematics lover, kalian pasti tau kan hipnotis?
Nah,gambar kali ini menguji kalian menggunakan imajinasmu
untuk melihat sesuatu yang aneh,
seperti apakah?
Ini dia...Coba kalian perhatikan titik yang ada di tengah dengan seksama.
Sudah itu, kalian gerakkan kepala kalian maju mundur.
Apa yang mathematics lover lihat?
Rantainya bergerak kan?
Nah,seperti hipnotis kan?
Buktinya mathematics lover nurut nurut aja tu disuruh
gerak-gerakkan kepala,iya kan?
Ayo ngaku!!!
Lanjut,sekarang lihat gambar ini.
Nah,ini khusus bagi mathematics lovers yang tajam penglihatannya.
Kalau mathematics lover perhatikan sesaat hanya terlihat gambar vas
bunga,iya toh?
Jika kita lihat dengan teliti dari sisi gelapnya,kita akan
melihat dua sisi wajah bule alias orang asing,
Bisa lihat nggak mathematics lovers?
Ok,mathematics lover ada yang suka kelinci nggak?
Atau ada yang suka bebek nggak?
Nah ternyata kelinci ama bebek nggak jau2 beda lo...
Percaya nggak???
Ya nggak lah,masak percaya?kalau percaya berarti menduakan tuhan...
hehehe...
Nah ini dia gambarnya...
Ok Mathematics lover sampai disini dulu kita berimajinasi,
Bagi mathematics lover yang punya komentar bisa post comment di blog ini.
See you again!!!
Kamis, 01 Maret 2012
A. SUDUT SALING BERPELURUS(BERSUPLEMEN)
Perhatikan gambar berikut ini.
Pada gambar di atas, garis AB adalah garis lurus sehingga besar ∠ AOB=180°.
Pada garis AB, dari titik O ditarik garis melalui C sehingga terbentuk sudut AOC dan sudut BOC. Sudut AOC merupakan pelurus atau suplemen dari sudut BOC.Demikian sebaliknya, sudut BOC adalah pelurus/ suplemen dari sudut AOC, sehingga diperoleh
∠ AOC+ ∠ BOC= ∠ AOB
a°+ b° = 180°
Atau dapat ditulis a°= 180° - b° dan b° = 180° - a°.
Jumlah dua sudut yang saling berpelurus ( bersuplemen) adalah 180°.
Sudut yang satu adalah pelurus dari sudut yang lainnya.
B.SUDUT SALING BERPENYIKU(BERKOMPLEMEN)
Pada gambar di atas terlihat ∠ PQR merupakan sudut siku-siku, sehingga besar ∠ PQR= 90°.
Jika pada ∠ PQR ditarik garis dari titik sudut Q akan terbentuk dua sudut yaitu sudut ∠ PQS dan sudut ∠ RQS. Dengan demikian ∠ PQS merupakan penyiku ( komplemen) dari ∠ RQS , demikian pula sebaliknya.Sehingga diperoleh
∠ PQS+ ∠ RQS= ∠ PQR
x°+ y° = 90°.
Atau dapat ditulis x°= 90° - y° dan y° = 90° - x°.
Jumlah dua sudut yang saling berpenyiku ( berkomplemen) adalah 90°. Sudut yang satu adalah penyiku dari sudut yang lainnya.
C.PASANGAN SUDUT SALING BERTOLAK BELAKANG
Perhatikan gambar berikut.
Pada gambar di atas garis KM dan LN saling berpotongan di titik O.
Dua sudut yang letaknya saling membelakangi disebut dua sudut yang saling bertolak belakang sehingga diperoleh,
∠ KON bertolak belakang dengan ∠ LOM ; dan
∠ NOM bertolak belakang dengan ∠ KOL.
Bagaimana besar sudut yang saling bertolak belakang?
Kita akan tahu jawabannya dengan memperhatikan hal berikut.
∠ KOL+ ∠ LOM =180° ( berpelurus)
∠ KOL=180°-∠ LOM (i )
∠ NOM+ ∠ KON= 180° ( berpelurus)
∠ NOM=180°-∠ LOM (ii )
Dari persamaan (i ) dan (ii) diperoleh,
∠ KOL=∠ NOM=180°- ∠ LOM
Jadi, besar ∠ KOL= ∠ NOM
Jika dua garis berpotongan maka dua sudut yang letaknya saling membelakangi titik potongnya disebut dua sudut yang saling bertolak belakang. Dua sudut yang saling bertolak belakang adalah sama besar.
EXERCISE FOR YOU
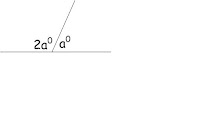
1. Perhatikan gambar berikut.
tentukan nilai a!
SOLUSI:
a°+ 2a° = 180°
3a° = 180°
a° = 180°: 3
a = 60.
2.Perhatikan gambar berikut.
tentukan nilai b!
SOLUSI:
90°+ b° +37° = 180°
127°+ b° = 180°
b° = 180° -127°
b° = 53°.
3. Perhatikan gambar berikut.
tentukan nilai c!
SOLUSI:
c°+c°+c° = 180°
3c° = 180°
c° = 180°:3
c° = 60°.
4. Perhatikan gambar berikut.
tentukan nilai d.
SOLUSI:
2d°+(d+40)°=180°
3d° +40° =180°
3d° =180°-40°
3d° =140°
d° =140°:3
d° = 46,67°
5. Perhatikan gambar berikut.
tentukan nilai e.
SOLUSI:
e = 41 (bertolak belakang).
6. Perhatikan gambar berikut.
tentukan nilai f.
SOLUSI:
f°+f°+f°+f°+f°+f°=360°
6f° = 360°
f° = 360°:6
f° = 60°
f = 60.
SELAMAT BELAJAR!!!
Perhatikan gambar berikut ini.
Pada gambar di atas, garis AB adalah garis lurus sehingga besar ∠ AOB=180°.
Pada garis AB, dari titik O ditarik garis melalui C sehingga terbentuk sudut AOC dan sudut BOC. Sudut AOC merupakan pelurus atau suplemen dari sudut BOC.Demikian sebaliknya, sudut BOC adalah pelurus/ suplemen dari sudut AOC, sehingga diperoleh
∠ AOC+ ∠ BOC= ∠ AOB
a°+ b° = 180°
Atau dapat ditulis a°= 180° - b° dan b° = 180° - a°.
Jumlah dua sudut yang saling berpelurus ( bersuplemen) adalah 180°.
Sudut yang satu adalah pelurus dari sudut yang lainnya.
B.SUDUT SALING BERPENYIKU(BERKOMPLEMEN)
Pada gambar di atas terlihat ∠ PQR merupakan sudut siku-siku, sehingga besar ∠ PQR= 90°.
Jika pada ∠ PQR ditarik garis dari titik sudut Q akan terbentuk dua sudut yaitu sudut ∠ PQS dan sudut ∠ RQS. Dengan demikian ∠ PQS merupakan penyiku ( komplemen) dari ∠ RQS , demikian pula sebaliknya.Sehingga diperoleh
∠ PQS+ ∠ RQS= ∠ PQR
x°+ y° = 90°.
Atau dapat ditulis x°= 90° - y° dan y° = 90° - x°.
Jumlah dua sudut yang saling berpenyiku ( berkomplemen) adalah 90°. Sudut yang satu adalah penyiku dari sudut yang lainnya.
C.PASANGAN SUDUT SALING BERTOLAK BELAKANG
Perhatikan gambar berikut.
Pada gambar di atas garis KM dan LN saling berpotongan di titik O.
Dua sudut yang letaknya saling membelakangi disebut dua sudut yang saling bertolak belakang sehingga diperoleh,
∠ KON bertolak belakang dengan ∠ LOM ; dan
∠ NOM bertolak belakang dengan ∠ KOL.
Bagaimana besar sudut yang saling bertolak belakang?
Kita akan tahu jawabannya dengan memperhatikan hal berikut.
∠ KOL+ ∠ LOM =180° ( berpelurus)
∠ KOL=180°-∠ LOM (i )
∠ NOM+ ∠ KON= 180° ( berpelurus)
∠ NOM=180°-∠ LOM (ii )
Dari persamaan (i ) dan (ii) diperoleh,
∠ KOL=∠ NOM=180°- ∠ LOM
Jadi, besar ∠ KOL= ∠ NOM
Jika dua garis berpotongan maka dua sudut yang letaknya saling membelakangi titik potongnya disebut dua sudut yang saling bertolak belakang. Dua sudut yang saling bertolak belakang adalah sama besar.
EXERCISE FOR YOU
1. Perhatikan gambar berikut.
tentukan nilai a!
SOLUSI:
a°+ 2a° = 180°
3a° = 180°
a° = 180°: 3
a = 60.
2.Perhatikan gambar berikut.
tentukan nilai b!
SOLUSI:
90°+ b° +37° = 180°
127°+ b° = 180°
b° = 180° -127°
b° = 53°.
3. Perhatikan gambar berikut.
tentukan nilai c!
SOLUSI:
c°+c°+c° = 180°
3c° = 180°
c° = 180°:3
c° = 60°.
4. Perhatikan gambar berikut.
tentukan nilai d.
SOLUSI:
2d°+(d+40)°=180°
3d° +40° =180°
3d° =180°-40°
3d° =140°
d° =140°:3
d° = 46,67°
5. Perhatikan gambar berikut.
tentukan nilai e.
SOLUSI:
e = 41 (bertolak belakang).
6. Perhatikan gambar berikut.
tentukan nilai f.
SOLUSI:
f°+f°+f°+f°+f°+f°=360°
6f° = 360°
f° = 360°:6
f° = 60°
f = 60.
SELAMAT BELAJAR!!!